You have been looking to buy a pair of shoes and notice that on Saturday they are marked down 20% from the original price. They are still too expensive! On Tuesday the shoes are marked down with an additional 25% off the price from Saturday. They are now $63. (a) What was the original price? (b) How much did you save? (c) What fraction of the original price did you spend?
Answers
(a) The original price of the shoes was $100.
(b) You saved $37.
(c) You spent 63/100 = 0.63 or 63% of the original price.
Related Questions
Eren constructed a rectangular paper box with a volume of 180in. His box has a length of x inches, a width of 5 inches less than its length, and a height 2 inches more than its length. What is the length of the box?
A. 7.52 in
B. 9.52 in
C. 5 in
D. 2.52 in
Answers
We know that the volume of a rectangular box is given by length times width times height. So, we have:
V = x * (x - 5) * (x + 2) = 180
Briefly defined, what is rectangle?
A rectangle is a sort of quadrilateral with parallel sides that are equal to one another and four vertices that are all 90 degrees apart. Because of this, it is also known as an equiangular quadrilateral. Because the opposite sides of a rectangle are equal and parallel, it can also be referred to as a parallelogram.
We can use this equation to find the length of the box.
Expanding the equation:
x^3 - 5x^2 + 2x = 180
Solving for x using a calculator or an algebraic equation solver we can find that x = 9.52
So the length of the box is 9.52 inches.
The answer is B. 9.52 in
Learn more about rectangle
brainly.com/question/2607596
#SPJ1
43. A Pop Warner football team had a total loss of 85 yards in penalties on 5 plays. Then triple their yards in penalties on the next 17 plays. What was the final yards the team loss?
Answers
Answer:
240 yards lost, if I understand the question correctly.
Step-by-step explanation:
If I read this correctly the team lost 85 yards lost in 8 plays. Then they tripled their loss on the next 17. 3 x 85 = 255 yards lost in the last 17 plays.
Total yards lost was (85 + 255) = 240 yards in 22 plays.
Quadrilateral WXYZ is a rectangle. Find each measure if m<1 = 30 . (Lesson 6-4 )
m<8
Answers
In a rectangle WXYZ, if the measure of angle 1 is 30 degrees, then the measure of angle 8 can be determined.
A rectangle is a quadrilateral with four right angles. In a rectangle, opposite angles are congruent, meaning they have the same measure. Since angle 1 is given as 30 degrees, angle 3, which is opposite to angle 1, also measures 30 degrees.
In a rectangle, opposite angles are congruent. Since angle 1 and angle 8 are opposite angles in quadrilateral WXYZ, and angle 1 measures 30 degrees, we can conclude that angle 8 also measures 30 degrees. This is because opposite angles in a rectangle are congruent.
Since angle 3 and angle 8 are adjacent angles sharing a side, their measures should add up to 180 degrees, as they form a straight line. Therefore, the measure of angle 8 is 180 degrees minus the measure of angle 3, which is 180 - 30 = 150 degrees.
So, if angle 1 in rectangle WXYZ is 30 degrees, then angle 8 measures 150 degrees.
Learn more about rectangle here:
https://brainly.com/question/29123947
#SPJ11
The ceiling of Katie's living room is a square that is 15 ft long on each side. To decorate for a party, she plans to hang crepe paper around the perimeter of the ceiling and then from each corner to the opposite corner. Katie can buy rolls that each contain 20 ft of crepe paper. What is the minimum number of rolls she should buy? Show your work.
Answers
Answer:
3
Step-by-step explanation:
Steps to answering this question : Determine the perimeter of the ceiling Divide the perimeter of the ceiling by the length of the rolls of crepe paperPerimeter of square = 4l
Where l = length of a side
4 x 15 feet = 60 feet
60/20 = 3
Answer:
6
Step-by-step explanation:
took test
Sal is trying to determine which cell phone and service plan to buy for his mother. The first phone costs $100 and $55 per month for unlimited usage. The second phone costs $150 and $51 per month for unlimited usage. How many months will it take for the second phone to be less expensive than the first phone?
Answers
Answer:
It takes 13 months for the second phone to be less expensive than the first phone.
Step-by-step explanation:
First phone: y = 100 + 55x
Second phone: y = 150 + 51x
(x = number of months, y = total cost)
Make a T-Chart.
First phone: Second phone:
x | y x | y
0 | 100 0 | 150
1 | 155 1 | 201
2 | 210 2 | 252
3 | 265 3 | 303
4 | 320 4 | 354
5 | 375 5 | 405
6 | 430 6 | 456
7 | 485 7 | 507
9 | 595 9 | 609
10 | 650 10 | 660
11 | 705 11 | 711
12 | 760 12 | 762
13 | 815 13 | 813
After 13 months, the second phone will have costed $2 less than the first phone, and the price of the second will continue to be lower than the first.
Answer:
1st: 100+55x>150+51x
2nd: x>12.5
3rd: 13
Step-by-step explanation:
need help asap! giving brainliest!!

Answers
Answer:
c = 8.6
Step-by-step explanation:
a² + b² = c²
The length in x is 7
The rise in y is 5
7² + 5² = c²
49 + 25 = c²
74 = c²
Take the square root of both sides
c = 8.602325267
Rounded
c = 8.6
Someone please help me with my homework!! plzzzzz
y varies inversely with x. If y = 7 when x = -4, find y when x = 5.
Answers
Y=21
Step-by-step explanation:

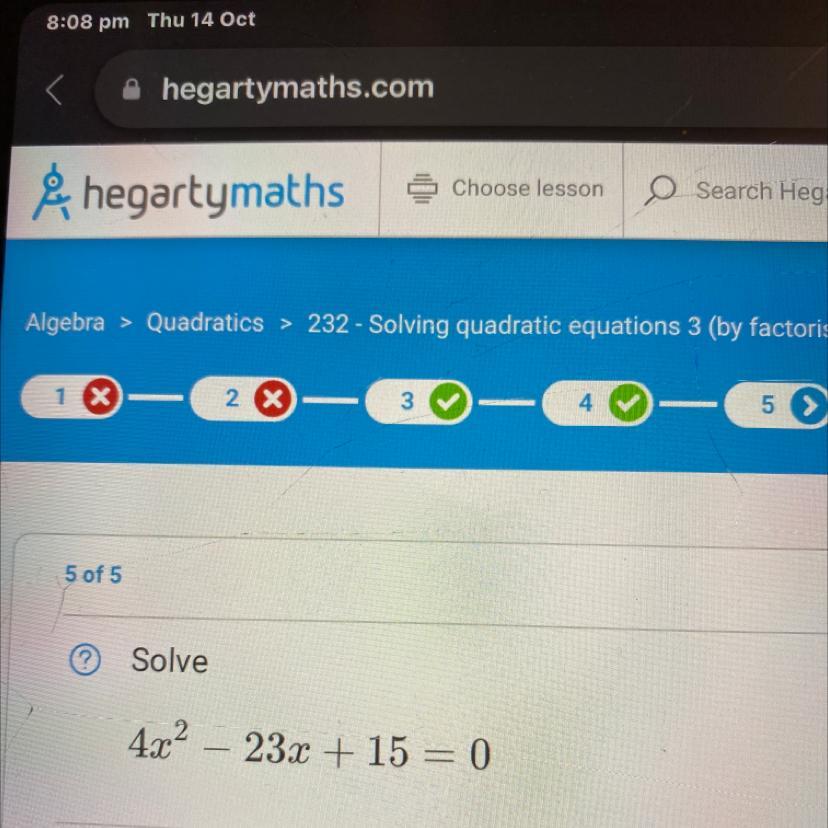
Please solve by factorising
Answers
Answer:
3/4 or 5
Step-by-step explanation:
Use the quadratic formula
Answer:
x = \(\frac{3}{4}\) , x = 5
Step-by-step explanation:
4x² - 23x + 15 = 0
Consider the factors of the product of the x² term and the constant term which sum to give the coefficient of the x- term.
product = 4 × 15 = 60 and sum = - 23
The factors are - 20 and - 3
Use these factors to split the x- term
4x² - 20x - 3x + 15 = 0 ( factor the first/second and third/fourth terms )
4x(x - 5) - 3(x - 5) = 0 ← factor out (x - 5) from each term
(x - 5)(4x - 3) = 0
Equate each factor to zero and solve for x
x - 5 = 0 ⇒ x = 5
4x - 3 = 0 ⇒ 4x = 3 ⇒ x = \(\frac{3}{4}\)
Solve for y:
-6+ 2y =12
Answers
Answer:
9
Step-by-step explanation:
-6+2y=12
+6 +6
2y=18
2 2
9
Is the mean greater than, less than, or equal to the median?

Answers
ANSWER: The mean is less than the median which in most cases is less than the mode. The mean is more accurate but if the question comes for a double exponential distribution the median is more accurate. Finally, the mean is greater than the mode if the distribution is positively skewed. If the mean is less than the mode, the distribution is negatively skewed. If the mean is greater than the median, the distribution is positively skewed.
Step-by-step explanation:
what is the last digit of 3 with a power of 2011
Answers
So to find any last digit of 3^2011 divide 2011 by 4 which comes to have 3 as remainder. Hence the number in units place is same as digit in units place of number 3^3. Hence answer is 7.
Jim and Elaine were driving from Toronto to Ottawa, a distance of 400 kilometres. Jim drove 1⁄4 of the way. Then Elaine took over and drove 1⁄2 of the remaining distance. How far did they still have to travel?
(a) 100 km (b) 150 km (c) 200 km (d) 50 km (e) none of these
could you explain the solution?
Answers
B)150 km
Step-by-step explanation:
The total distance is 400km
and jim drove 1/4 of this distance so
400 x 1/4 = 100km
then subtract this from the total distance 400 - 100 = 300km
Elaine drove 1/2 of this remaining distance
300 x 1/2 = 150 km
Add this with the first result
100 + 150 = 250 km
this is the total disrance that they have treveled
how much do they have to go
400 - 250 = 150km meaning the answer is b
solve the equation 3/x-4=1/5
Answers
Answer:
The very first thing we want to do in this equation is to isolate x on one side (preferably the left side).
3/x - 4 = 1/5
We get rid of any constants first, by performing the inverse property;
The inverse property of subtraction is addition, so we add 4 to both sides:
+4 +4
3/x = 4 1/5
3 is being divided by x, so the inverse operation of division is multiplication. So we multiply by 1/3 on both sides.
x1/3 x1/3
X = 1 4/10 which simplifies to 1 2/5.
There is a line whose slope is 0 and whose y-intercept is 2. What is its equation in slope-intercept form?
Answers
Answer:
\(y = 2 \)
Step-by-step explanation:
Given that ,
\( m = 0 \)\( y - intercept = 2 \)And we need to find out the equation of the line . We can use the slope intercept form of the line which is \(y=mx+c\) as ,
\(\implies y = mx + c \)
Substitute the values ,
\(\implies y = 0x + 2 \)
\(\\\implies \underline{\boxed{y = 2}} \)
which has more variation? group of answer choices the distribution of the sample means of size n the distribution of all x values
Answers
The distribution of the sample means of size n generally has less variation than the distribution of all individual x values.
When we calculate the sample mean, we take the average of a subset of data points from the population. By doing this, we are essentially reducing the variability compared to considering all individual values.
The Central Limit Theorem states that as the sample size increases, the distribution of sample means approaches a normal distribution, regardless of the shape of the population distribution. This means that the distribution of the sample means tends to be less variable and more tightly clustered around the true population mean.
On the other hand, the distribution of all individual x values can exhibit greater variation because it includes the entire range of values without the effects of averaging or reducing variability through sampling. It reflects the full extent of the variability in the data set, including outliers and extreme values.
In summary, the distribution of the sample means of size n typically has less variation compared to the distribution of all individual x values.
To learn more about mean visit;
https://brainly.com/question/31101410
#SPJ11
Luke and Seth each need to buy the same amount of fencing for their gardens. While Seth's garden is square in shape, Luke's garden is rectangular with the length 3 feet longer than Seth's. Luke's width is half of the length of his own garden.
How much fencing did each buy? Need this asap please and thank you.
option
40. 5 feet
81 feet
72 feet
36 feet
Answers
Fencing that Luke and Seth did each buy is 72 feet
Using the information given, you can set up and solve the system of equations. Let x be the length of Seth's garden.
Seth's garden is square, so it has four times the perimeter.
The perimeter of Luke's garden is a rectangle of length x + 3 feet and width x/2 feet, so 2(x + 3) + 2(x/2).
We also know that Luke and Seth should buy the same amount of fences. So:
4x = 2(x + 3) + 2(x/2)
Solving this equation for x gives x = 6 feet.
So Seth's yardage is 6 feet and Luke's yardage is 9 feet.
So the fence required for Seth's garden is 46 = 24 feet
and the fence required for Luke's garden is 2(9) + 2(9/2) = 29 + 2*4.5 = 36 + 9 = 45 It's feet.
So the total fencing required is 24 + 45 = 72 feet.
Learn more about length and width here: https://brainly.com/question/24571594
#SPJ4
Please please help me with this question ASAP ASAP please
Answers
the monthly utility bills in a city are normally distributed, with a mean of $100 and a standard deviation of $15. Find the probability that a randomly selected utility bill is (a) less than $68, (b) between $81 and $90, and (c) more than $120.
Answers
The probability that a randomly selected utility bill is,
a) P(X < 68) ≈ 0.016 or 1.6%
b) P(81 < X < 90) ≈ 0.1476 or 14.76%
c) P(X > 120) ≈ 0.0912 or 9.12%
To find the probability in each case, we can use the standard normal distribution by converting the given values into z-scores.
a) To find the probability that a randomly selected utility bill is less than $68, we need to find P(X < 68). First, we calculate the z-score using the formula z = (x - μ) / σ, where x is the value, μ is the mean, and σ is the standard deviation.
z = (68 - 100) / 15 = -2.1333
Using a standard normal distribution table or a calculator, we can find the corresponding cumulative probability for z = -2.1333, which is approximately 0.016. Therefore, the probability P(X < 68) is approximately 0.016 or 1.6%.
b) To find the probability that a randomly selected utility bill is between $81 and $90, we need to find P(81 < X < 90). We calculate the z-scores for both values:
z1 = (81 - 100) / 15 = -1.2667
z2 = (90 - 100) / 15 = -0.6667
Using the standard normal distribution table or a calculator, we find the cumulative probability for z1 and z2: P(z1) ≈ 0.1038 and P(z2) ≈ 0.2514. Then, we subtract P(z1) from P(z2) to find the probability between the two values:
P(81 < X < 90) ≈ P(z1 < Z < z2) ≈ P(z2) - P(z1) ≈ 0.2514 - 0.1038 ≈ 0.1476 or 14.76%.
c) To find the probability that a randomly selected utility bill is more than $120, we need to find P(X > 120). We calculate the z-score:
z = (120 - 100) / 15 = 1.3333
Using the standard normal distribution table or a calculator, we find the cumulative probability for z = 1.3333, which is approximately 0.9088. Since we want the probability of X to be greater than 120, we subtract this value from 1:
P(X > 120) ≈ 1 - P(z) ≈ 1 - 0.9088 ≈ 0.0912 or 9.12%.
Learn more about probability at
https://brainly.com/question/31828911
#SPJ4
Which is shorter? 3/6 of a minute or 2/6 of an hour?
Answers
Answer:
3/6 of a minute
Step-by-step explanation:
3/6 can also be simplified to 1/2. So, 1/2 of a minute is 30 seconds. 2/6 can be simplified to 1/3. So, 1/3 of an hour is 20 minutes. 30 seconds is very much shorter than 20 minutes. Thus, 3/6 of a minute is shorter than 2/6 fo an hour.
PLEASE HELP ME QUICKKKKK

Answers
It says the rocket was in the air for approximately 6 seconds before hitting the ground.
But the graph proves it untrue because after 6 seconds it is still in the air, rather than on the ground like (3) suggests.
Sam and Fatima won $2000 in the lottery. They agreed to divide the winnings in the ratio (Sam) 2 : 3 (Fatima). How much money did Sam receive? A. $800 B. $600 C. $1000 D. $1200
Answers
Answer:
D
Step-by-step explanation:
In total, there are 5 units (2 + 3). Then, divide 2000 by 5, which equals into 400. Finally, because Fatima takes 3 units, we use 400 times 3, making it D.
Can someone help me with this Question.

Answers
The formula we need to use is given above. In this formula, we will substitute the desired values. Let's start.
\(P=3W+D\)A) First, we can start by analyzing the first premise. The team has \(8\) wins and \(5\) losses. It earned \(8 \times 3 = 24\) points in total from the matches it won and \(1\times5=5\) points in total from the matches it drew. Therefore, it earned \(24+5=29\) points.
B) After \(39\) matches, the team managed to earn \(54\) points in total. \(12\) of these matches have ended in draws. Therefore, this team has won and lost a total of \(39-12=27\) matches. This number includes all matches won and lost. In total, the team earned \(12\times1=12\) points from the \(12\) matches that ended in a draw.
\(54-12=42\) points is the points earned after \(27\) matches. By dividing \(42\) by \(3\) ( because \(3\) points is the score obtained as a result of the matches won), we find how many matches team won. \(42\div3=14\) matches won.
That leaves \(27-14=13\) matches. These represent the matches team lost.
Finally, the answers are below.
\(A)29\)
\(B)13\)
Answer:
a) 29 points
b) 13 losses
Step-by-step explanation:
You want to know points and losses for different teams using the formula P = 3W +D, where W is wins and D is draws.
A 8 wins, 5 drawsThe number of points the team has is ...
P = 3W +D
P = 3(8) +(5) = 29
The team has 29 points.
B 54 pointsYou want the number of losses the team has if it has 54 points and 12 draws after 39 games.
The number of wins is given by ...
P = 3W +D
54 = 3W +12
42 = 3W
14 = W
Then the number of losses is ...
W +D +L = 39
14 +12 +L = 39 . . . substitute the known values
L = 13 . . . . . . . . . . subtract 26 from both sides
The team lost 13 games.
__
Additional comment
In part B, we can solve for the number of losses directly, using 39-12-x as the number of wins when there are x losses. Simplifying 3W +D -P = 0 can make it easy to solve for x. (In the attached, we let the calculator do the simplification.)
<95141404393>

Which of the following differential equation(s) is/are linear? (Choose all that apply.) 1 2xy" - 5xy' + y = sin(3x) (v)² + xy =In(x) □y' + sin(y)=e3x (x²+1)y"-3y - 2x³y=-x-9 (+1)y'+xy=y"
Answers
To determine which differential equation(s) are linear, we need to examine the form of each equation. A linear differential equation is one that can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x), b(x), c(x), and g(x) are functions of x.
The differential equation 2xy" - 5xy' + y = sin(3x) is linear. It can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x) = 2x, b(x) = -5x, c(x) = 1, and g(x) = sin(3x).
The differential equation (v)² + xy = In(x) is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (v)², where v represents the derivative of y with respect to x. This term does not have a linear coefficient.
The differential equation y' + sin(y) = e^(3x) is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = sin(y), and g(x) = e^(3x).
The differential equation (x²+1)y" - 3y - 2x³y = -x - 9 is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (x²+1)y", where the coefficient is a function of x.
The differential equation y' + xy = y" is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = x, and g(x) = y".
Learn more about differential equation here
https://brainly.com/question/32524608
#SPJ11
In the figure below, each charged particle is located at one of the four vertices of a square with side length =a. In the figure, A=4,B=2, and C=5, and q>0. (i) (a) What is the expression for the magnitude of the electric field in the upper right corner of the square (at the location of q )? (Use the following as necessary: q, and k
e
.) E= Give the direction angle (in degrees counterclockwise from the +x-axis) of the electric field at this location. ' (counterclockwise from the +x-axis) (b) Determine the expression for the total electric force exerted on the charge q. (Enter the magnitude. Use the following as necessary: q, and k
e
.) F= Give the direction angle (in degrees counterclockwise from the +x-axis) of the electric force on q. - (counterclockwise from the +x-axis) (c) What If? How would the answers to parts (a) and (b) change if each of the four charges were negative with the same magnitude? Select all that apply. The force would be the same magnitude but opposite direction as the force in part (b). The electric field would be the same magnitude and direction as the field in part (a). The electric field would be the same magnitude but opposite direction as the field in part (a). The force would be the same magnitude and direction as the force in part (b).
Answers
a) The expression for the magnitude of the electric field at the upper right corner of the square is E = (k_e * 4) / (a^2 * 2) + (k_e * 5) / a^2
b)The expression for the total electric force exerted on the charge q is given by:
F = q * [(k_e * 4) / (a^2 * 2) + (k_e * 5) / a^2]
(a) To find the expression for the magnitude of the electric field at the upper right corner of the square, we need to consider the contributions from charges A and C.
The electric field due to a point charge is given by the equation:
E = k_e * (q / r^2)
where E is the electric field, k_e is the electrostatic constant, q is the charge, and r is the distance from the charge.
For the upper right corner, the distance from charge A is a√2, and the distance from charge C is a.
Therefore, the expression for the magnitude of the electric field at the upper right corner is:
E = (k_e * A) / (a√2)^2 + (k_e * C) / a^2
Substituting the given values A = 4 and C = 5, we have:
E = (k_e * 4) / (a^2 * 2) + (k_e * 5) / a^2
(b) The expression for the total electric force exerted on the charge q is given by:
F = q * E
where F is the force and q is the charge. Substituting the expression for the electric field from part (a), we have:
F = q * [(k_e * 4) / (a^2 * 2) + (k_e * 5) / a^2]
(c) If each of the four charges were negative with the same magnitude, the answers to parts (a) and (b) would change as follows:
The force would be the same magnitude but opposite direction as the force in part (b).
The electric field would be the same magnitude but opposite direction as the field in part (a).
In other words, the signs of both the electric field and force would be reversed. The magnitudes, however, would remain the same.
To learn more about electric field
https://brainly.com/question/19878202
#SPJ11
solve elimination method
3x+2y-15=0
5x-3y -25=0
Answers
Answer:
x=5
y=0
Step-by-step explanation:
3x+2y−15=0
5x−3y−25=0
multiply the first equation by 3, and multiply the second equation by 2.
3(3x+2y−15=0)
2(5x−3y−25=0)
becomes:
9x+6y−45=0
10x−6y−50=0
add these equations to eliminate y:
19x−95=0
Then solve 19x−95=0 for x:
19x−95=0
19x−95+95=0+95 (add 95 to both sides)
19x=95
19x
19
=
95
19
(divide both sides by 19)
x=5
now that we've found x let's plug it back in to solve for y.
write down an original equation:
3x+2y−15=0
substitute 5for x in 3x+2y−15=0:
(3)(5)+2y−15=0
2y=0 (simplify both sides of the equation)
2y
2
=
0
2
(divide both sides by 2)
y=0
factor the expression using the GCF 8x+20y= ( x+ y)
Answers
9514 1404 393
Answer:
4(2x +5y)
Step-by-step explanation:
The variables x and y have no common factors. The coefficients 8 and 20 have a common factor of 4. So, the expression can be written ...
4(2x +5y)
a cashier cannot tell the difference between cilantro and parsley. customers would only buy either cilantro or parsley. he knows that 20% of his customers prefer parsley. these customers will buy parsley 40% of the time when shopping. otherwise, they wouldn't buy either herb. 40% of his customers prefer cilantro and will buy cilantro 15% of the time when shopping. otherwise, they wouldn't buy either herb. the other 40% of his customers don't prefer, and thus don't buy, either herb. given the next customer buys one of the two herbs, what is the probability it is parsley?
Answers
Probability that customer buy parsley given buy any of two herb
= 0.5714
What is probability in math?
Probability refers to potential. The subject of this area of mathematics is the occurrence of random events.The range of the value is 0 to 1. To forecast how likely events are to occur, probability has been introduced in mathematics.Parsley ( 0.4 , 0.6 )
buy = B ∩ P = 0.08
Don't buy = DB ∩ P = 0.12
Cilantro = ( 0.15 , 0.85 )
buy = B ∩ C = 0.06
Don't buy = DB ∩ C = 0.34
Don't buy anything = DB = 0.4
P( Buy anything ) = P(B∩P) + P( B ∩ C )
= 0.08 + 0.06 = 0.14
Now, P( P/B) = P( P ∩ B)/P(B)
= 0.08/0.14 = 4/7 = 0.5714
Hence, probability that customer buy parsley given buy any of two herb
= 0.5714
Learn more about probability
brainly.com/question/11234923
#SPJ4
Two basketball players are trying to have the most points per game for the season. The current leader has 2112 points in 77 games and the second place player has 2020 in 74 games. How many points per game did the second place team team score? Round to the nearest tenth
Answers
Answer:
27.3 points per game
Step-by-step explanation:
2020/74 = 27.3 points per game
what is the probability that a standard normal random variable will be between .3 and 3.2?
Answers
According to the z table, there is a 0.3814 percent chance that such a standard normal random variable would fall between 0.3 and 3.2.
What is the probability?
The possibility of an event occurring is stated as a number between 0 and 1, where 0 indicates that the event cannot occur and 1 indicates that the event is guaranteed to occur. The probability of an event A is defined mathematically as the number of positive outcomes divided by the total number of alternative outcomes.
We must determine the likelihood that a standard normal random variable would occur with a probability between 0.3 and 3.2.
First, a standard normal random variable with a mean and standard deviation is introduced.
We must determine the likelihood that a standard normal random variable will fall within the range of 0.3 and 3.2.
The probability therefore should be
P(0.3<z<3.2)=P(z<3.2)−P(z<0.3)
Using z's typical value
P(0.3<z<3.2)=0.9993−0.6179
P(0.3<z<3.2)=0.3814
Therefore, there is a 0.3814 percent chance that a standard normal random variable would fall between 0.3 and 3.2.
To know more about standard normal random variable visit:
brainly.com/question/14782203
#SPJ4
Please help me with these, im really confused so i’ll be very grateful and appreciate for everything.

Answers
If DE is the mid segment in the figure the vales of x are
7. x = 68. x = 89. x = 1310. x = 10How to solve for xThe value of x is solved using the concept of similar triangles and remembering that DE is the mid segment making the points as the opposite sides of DE equal
The proportions is solved as follows
9. x / 26 = 1 / 2
2x = 26
x = 13
Also
10. 5 / x = 1 / 2
x = 5 * 2
x = 10
Learn more about similar triangles at:
https://brainly.com/question/2644832
#SPJ1