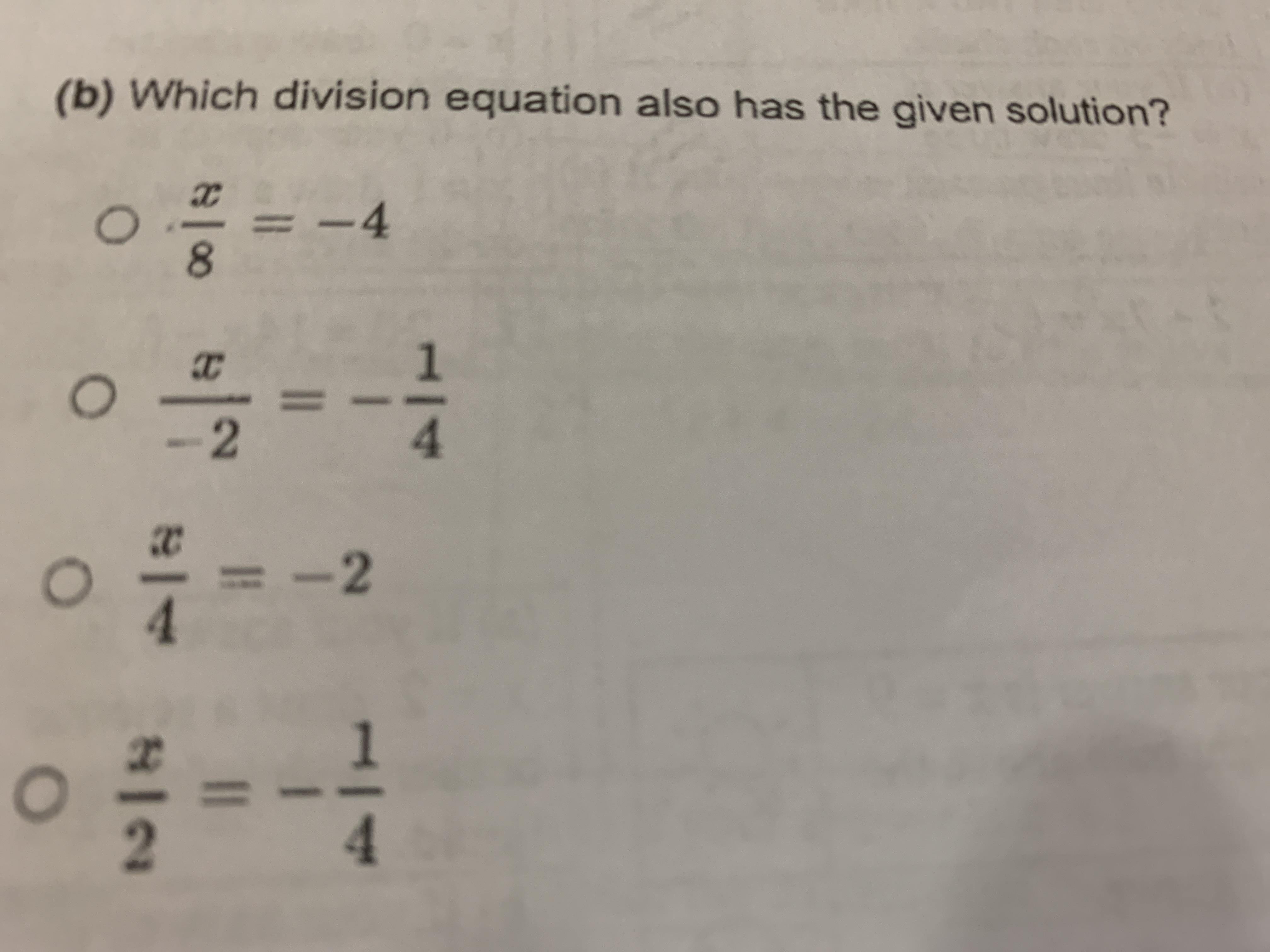Answers
Answer:
\(\frac{x}{2} = -\frac{1}{4}\)
Step-by-step explanation:
To isolate the x, multiply both sides by the numerator. For example, in the equation \(\frac{x}{2} = -\frac{1}{4}\), multiply both sides by 2 to get \(2* \frac{x}{2} = 2 * -\frac{1}{4}\), so x = \(-\frac{1}{2}\).
Related Questions
2 x 2 x 2 x 7 is the prime factorization of what number?? please help :(
Answers
Answer:
2×2×2×7
Step-by-step explanation:
if you multply 2×2 it is 4×2=8×7=56
backward is easy 7×2= 14×2= 28×2=56
2 × 2 × 2 × 7 is the prime factorization of the number 56.
Given that,
To determine the number whose prime factorization is given as 2 x 2 x 2 x 7.
What is the factors?
Factors can be defined by splitting the value into multipliable values.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Prime factorization of the number are a multiplicable number that consists of the prime numbers only,
According to the question,
2 x 2 x 2 x 7 = 56
Thus, 2 × 2 × 2 × 7 is the prime factorization of the number 56.
Learn more about simplification here: https://brainly.com/question/12501526
#SPJ3
The number of pages read varies directly as the number of minutes spent reading. After 20 minutes, Zack had read 12 pages. How many pages can Zack read in 35 minutes? Do not include units in your answer.
Answers
First, make a proportion
12 pages x pages
—————— = ——————
20 minutes 35 minutes
Second, cross multiple
20x=420
Simplify by dividing both sides by 20
x=21 pages
Hope this helps!
Answer:
21
Step-by-step explanation:
find the coordinates of the points of intersection of the graph y=13-x with the axes. Find the area of the right triangle formed by this line and the coordinate axis
Answers
Answer:
Y(0,13)
X(13,0)
Select the correct answer from each drop-down menu. The gasoline prices in seven states are $1.96, $2.09, $1.79, $1.61, $1.75, $2.11, and $1.84. The median gasoline price is _____. The difference of the first and third quartiles in this set of gas prices is ______ .
Answers
Answer:
The median is 1.84 and the difference between the first and third quartile is 0.34
Step-by-step explanation:
When you write them out 1.84 is the median (middle number). To find the difference I just subtracted the third quartile (2.09) by the first quartile (1.75)
========================================================
Explanation:
Original data set = {1.96, 2.09, 1.79, 1.61, 1.75, 2.11, 1.84}
Sorted data set = {1.61, 1.75, 1.79, 1.84, 1.96, 2.09, 2.11}
Notice that 1.84 is in the middle of the sorted set. Three values are smaller than it, and three values are larger than it.
Therefore, 1.84 is the median.
The values {1.61, 1.75, 1.79} are smaller than the median. We'll call this set L for lower set.
The values {1.96, 2.09, 2.11} are larger than the median. We'll call this set U for upper set.
From set L = {1.61, 1.75, 1.79}, the median here is 1.75. This is the value of the first quartile Q1
The value of Q3 is 2.09 as it is in the direct middle of set U = {1.96, 2.09, 2.11}
The interquartile range (IQR) is the difference of Q3 and Q1
IQR = Q3 - Q1
IQR = 2.09 - 1.75
IQR = 0.34
What does the circled portion represent in the confidence interval formula?
p±z.
O Sample proportion
O Margin of error
p(1-p)
n
Confidence interval
O Sample Size
Answers
The circled portion in the confidence interval formula p ± z represents the Margin of Error, which plays a crucial role in interpreting the range of plausible values for the population parameter.
In the confidence interval formula p ± z, the circled portion represents the Margin of Error.
The Margin of Error is a critical component of a confidence interval and quantifies the level of uncertainty in the estimate.
It indicates the range within which the true population parameter is likely to fall based on the sample data.
The Margin of Error is calculated by multiplying the critical value (z) by the standard deviation of the sampling distribution.
The critical value is determined based on the desired level of confidence, often denoted as (1 - α), where α is the significance level or the probability of making a Type I error.
The Margin of Error accounts for the variability in the sample and provides a measure of the precision of the estimate.
It reflects the trade-off between the desired level of confidence and the width of the interval.
A larger Margin of Error indicates a wider confidence interval, implying less precision and more uncertainty in the estimate.
Conversely, a smaller Margin of Error leads to a narrower confidence interval, indicating higher precision and greater certainty in the estimate.
For similar question on confidence interval.
https://brainly.com/question/29576113
#SPJ11
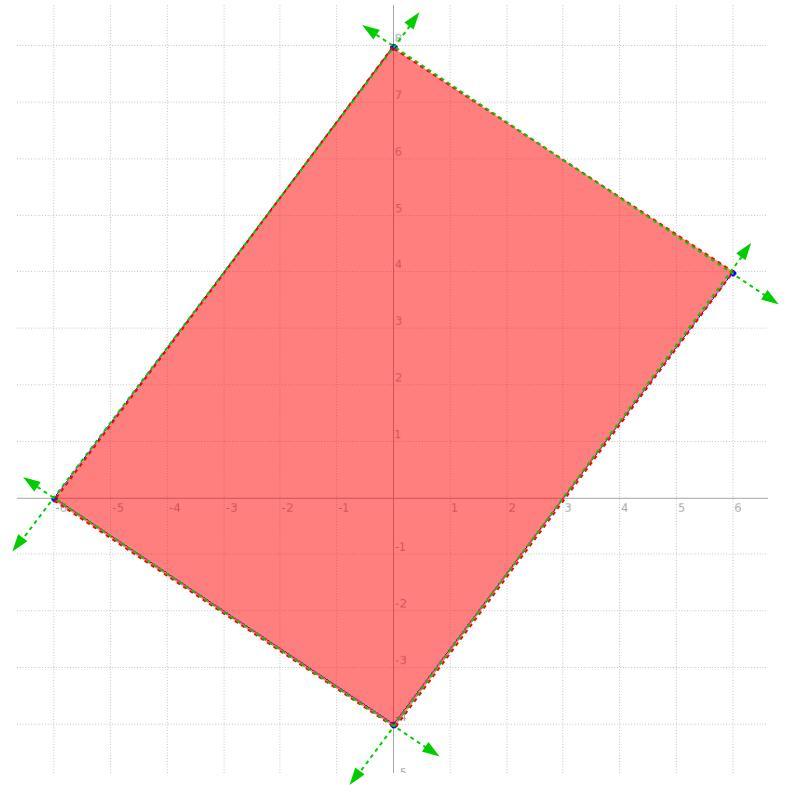
HELP PLEASE I DONT GET THIS

Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
2. If Jon took a test and made the following scores: 72, 84, 92, 80, 96, 88, 45, 70, 79, 92, 87, and 103.
a. Box and Whisker plot:
b. What is the range:
IQR:
c. Are there any outliers?
3. If the mean is 77 and the standard deviation is 11 please find:
a.
A value 3 standard deviations above the mean
b.
A value 2.5 standard deviation below the mean
c. A value 2 standard deviations below the mean
d. A value 1 standard deviation above the mean
4. If 99.7 percent of the data is between 30 and 90, then please find the mean and the standard of deviation.
b. o:
a. u
5. If 68 percent of the data is between 42 and 58, then please find the mean and the standard of deviation.
b. a:
a. p
6. If 95 percent of the data is between 34 and 64, then please find the mean and the standard of deviation.
b. a:
a. µ
Someone please help with this page

Answers
Answer:
a)
103
|
96 +
|
92 | *
| * *
88 +--*
| *
84 |
|*
80 +
|
79 |
|
72 +
|
70 |
|
b)b. The range is the difference between the highest and lowest scores: 103 - 45 = 58.
The IQR is the interquartile range, which is the range of the middle 50% of the scores. To find it, we first need to find the first and third quartiles:
The first quartile (Q1) is the median of the lower half of the scores, which are 45, 70, 72, 79, and 80. The median of this set is (72+79)/2 = 75.5.
The third quartile (Q3) is the median of the upper half of the scores, which are 84, 87, 88, 92, and 96. The median of this set is (88+92)/2 = 90.
Therefore, the IQR is 90 - 75.5 = 14.5.
c)c. To find any outliers, we need to first define the "fences" of the box and whisker plot. The lower fence is Q1 - 1.5IQR = 75.5 - 1.514.5 = 53.25. The upper fence is Q3 + 1.5IQR = 90 + 1.514.5 = 112.75.
There is one score that is outside the fences: 103. Therefore, 103 is an outlier.
Step-by-step explanation:
please assist with these questions thanks



Answers
1a. The percentage total return is -19.56%
1b. The dividend yield is 2.42%.
1c. The capital gains yield is -21.98%.
2a. The arithmetic average annual return on large-company stocks in nominal terms is 14.5%.
2b. The arithmetic average annual return on large-company stocks in real terms is 9.67%.
3a. The real return on long-term government bonds is 3.195%
3b. The real return on long-term corporate bonds is 3.291%
How to calculate the percentage total return?In Financial accounting, the percentage total return (P) can be calculated by using this formula;
P = [(Ending price - Initial price) + Dividend] ÷ Initial price
P = [(71 - 91) + 2.20] ÷ 91
P = -0.1956 or -19.56%
1b. For the dividend yield, we have:
Dividend yield = Dividend ÷ Initial price
Dividend yield = 2.20 ÷ 91
Dividend yield = 0.0242 or 2.42%
1c. For capital gains yield, we have:
Capital gains yield = (Ending price - Initial price) ÷ Initial price
Capital gains yield = (71 - 91) ÷ 91
Capital gains yield = -0.2198 or -21.98%.
Part 2.
a. The arithmetic average of annual return on large-company stocks in nominal terms is equal to 14.5%.
b. For arithmetic average annual return in real terms, we have:
(1 + 0.145) = (1 + r)(1 + 0.044)
r = (1.145/1.044) - 1
r = 9.67%
Part 3.
a. For real return on the long-term government bonds, we would apply Fisher equation:
(1 + i) = (1 + r)(1 + h)
Where:
i is the nominal interest rate.r is the real interest rate.h is the inflation rate.(1 + 0.066) = (1 + r)(1 + 0.033)
1 + r = 1.066/1.033
r = 3.195%
b. For real return on long-term corporate bonds:
(1 + 0.067) = (1 + r)(1 + 0.033)
1 + r = 1.067/1.033
r = 3.291%
Learn more about real return and stocks here: https://brainly.com/question/32228847
#SPJ1
FOR BRAINIEST PLEASE ANSWER ASAP

Answers
To do so, we must find the slope (m), which represents the linear rate of change, so let’s choose two ordered pairs and plug them into the slope formula.
Ordered pairs (x, y)——>(miles traveled, total fee)
(2, 17) and (5, 21.50)
Slope formula:
m=(y₂ - y₁)/(x₂ - x₁)
Plug in the ordered pairs from above:
m=(21.5-17)/(5-2)
Simplify:
m=4.5/3
m=1.5
So, the rate is $1.5 per mile. To determine the y-intercept (if there is one), we used a point we already have and input x into the equation and determine how y is formed.
We currently have the equation: y=1.5x+b, where b=y-intercept and is unknown currently.
Let’s plug in the first ordered pair: (2, 17). We will then solve for b.
(17)=1.5(2)+b
Simplify:
17=3+b
Solve for b (y-intercept):
Subtract 3 from both sides:
17-3=b
14=b; b=14
So, we now have a y-intercept of 14. Let’s complete the equation now that we have all the information:
y=1.5x+14
Let’s input two ordered pairs into the equation again to assure we’re correct. For simplicity, we’ll use (2, 17) and (5, 21.50):
(17)=1.5(2)+14
Simplify:
17=3+14
17=17
Now, the second ordered pair:
(21.5)=1.5(5)+14
Simplify:
21.5=7.5+14
21.5=21.5
So, we are correct with the equation.
This means that answer is: the first option - “When the cab travels 0 miles, the fee is $14.00.”
Solve the following system of equations: {−6x−y=2−7x−4y=−9
Answers
Answer:
x=-1, y=4. (-1, 4).
Step-by-step explanation:
-6x-y=2
-7x-4y=-9
----------------
y=-6x-2
-7x-4(-6x-2)=-9
-7x+24x+8=-9
17x=-9-8
17x=-17
x=-17/17
x=-1
-6(-1)-y=2
6-y=2
y=6-2=4
A state university is interested in where its students come from. They survey 300 of its students to find out if they are in-state, out-of-state, or foreign students. Match the vocabulary word with its corresponding example.
Answers
In-state corresponds to students who are residents of the same state as the university, out-of-state corresponds to students from different states, and foreign corresponds to students from countries other than the university's country.
To match the vocabulary word with its corresponding example in the context of the state university survey, we need to understand the terms and their meanings.
Here are the vocabulary words and their corresponding examples:
Vocabulary Word: In-state
Example: A student who is a resident of the same state where the university is located.
They pay lower tuition fees compared to out-of-state or foreign students.
Vocabulary Word: Out-of-state
Example: A student who is not a resident of the state where the university is located.
They typically pay higher tuition fees compared to in-state students.
Vocabulary Word: Foreign
Example: A student who is from a country other than the country where the university is located.
They are international students who may have different visa requirements and tuition fees.
To match these vocabulary words with their corresponding examples:
In-state: A student from the same state as the university, paying lower tuition fees.
Out-of-state: A student from a different state than the university, paying higher tuition fees.
Foreign: A student from a country other than the country where the university is located, with potential differences in visa requirements and tuition fees.
By associating each vocabulary word with its respective example, we can accurately describe the three categories of students based on their residency and origin in the context of the state university's survey.
For similar question on residents.
https://brainly.com/question/2621599
#SPJ8
A truck with 30-in.-diameter wheels is traveling at 50 mi/h.
Find the angular speed of the wheels in rad/min, "hint convert miles to inches & hours to minutes:
_________rad/min
How many revolutions per minute do the wheels make?
___________rpm
Answers
Answer:
A. the angular speed is 3771.4 rad/min
b. 5921 rpms
Step-by-step explanation: I just got this same question right on a test.
The cost of a movie ticket is $9.75, which is $36.25 less than a ticket to go to a concert. What is the cost of a ticket to the concert?
Answers
Answer: $46
Step-by-step explanation:
An island is located 48 miles N23°38'W of a city. A
freighter in distress radios its position as N11°26'E of the
island and N12° 16'W of the city. How far is the freighter
from the city?
Answers
The freighter is approximately 164.33 miles from the city.
How to determine how far is the freighter from the city?We can use the Law of Cosines to solve this problem. Let's label the distances as follows:
d: distance between the city and the freighter
x: distance between the city and the island
y: distance between the island and the freighter
First, we need to find x using the given coordinates:
N23°38'W is equivalent to S23°38'E, so we have:
cos(23°38') = x/48
x = 48cos(23°38') ≈ 42.67 miles
Next, we can use the coordinates of the freighter to find y:
N11°26'E is equivalent to E11°26'N, and N12°16'W is equivalent to S12°16'E. This means that the angle between the island and the freighter is:
23°38' + 11°26' + 12°16' = 47°20'
cos(47°20') = y/d
We can rearrange this equation to solve for y:
y = dcos(47°20')
Now we can use the Law of Cosines to solve for d:
d² = x² + y² - 2xy cos(90° - 47°20')
d² = 42.67² + (d cos(47°20'))² - 2(42.67)(d cos(47°20')) sin(47°20')
d² = 1822.44 + d² cos²(47°20') - 2(42.67)(d cos(47°20')) sin(47°20')
d² - d² cos²(47°20') = 1822.44 - 2(42.67)(d cos(47°20')) sin(47°20')
d² (1 - cos²(47°20')) = 1822.44 - 2(42.67)(d cos(47°20')) sin(47°20')
d² sin²(47°20') = 1822.44 - 2(42.67)(d cos(47°20')) sin(47°20')
d² = (1822.44 - 2(42.67)(d cos(47°20')) sin(47°20')) / sin²(47°20')
d ≈ 164.33 miles
Therefore, the freighter is approximately 164.33 miles from the city.
Learn more about Law of Cosines at https://brainly.com/question/30766161
#SPJ1
Find the length of the line joining A (3,5) and B (1,3)
Answers
Answer:
2√2 units.
Step-by-step explanation:
To find the length of the line joining points A(3, 5) and B(1, 3), we can use the distance formula. The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Substituting the coordinates of points A and B into the formula, we have:
d = sqrt((1 - 3)^2 + (3 - 5)^2)
= sqrt((-2)^2 + (-2)^2)
= sqrt(4 + 4)
= sqrt(8)
= 2sqrt(2)
Therefore, the length of the line joining points A and B is 2√2 units.
can someone help me? please

Answers
Answer:
Step-by-step explanation:
Answer to number 1 is a slope of -3 and the y=-3x-26 For number 2 the slope is 5 and y=5x+5 and for number 3 the slope is 2/3 and b is y=2/3x-20/3 for number 4 its 4 in the x section and 5 for the y section number 5 is --5 and for number 6 its -12. I found the slopes by using this formula y2-y1/x2-x1 and for the b I used y=mx+b and used one of the points to figure it out! I hope this helped out :3
help..
only if you know

Answers
Mario has $150 to spend on food for a party. He ordered pizzas that cost $8 each and bottles of soda that cost $2 each which inequality represents how much he can
spend without running out of money?
Answers
Answer:
8p + 2s <= 150
Step-by-step explanation:
Let p = number of a pizza.
Let s = price of a bottle of soda.
The inequality is
8p + 2s <= 150
If the observed (actual) y value is 10, and the predicted value is 14, what is the residual?
Answers
The residual value with an actual value of 10 and a predicted value of 14 will be 4. Then the correct option is D.
What is Algebra?The analysis of mathematical representations is algebra, and the handling of those symbols is logic.
PEMDAS rule means for the Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This rule is used to solve the equation in a proper and correct manner.
We know that the difference between the predicted value and to actual value is known as the residual value.
Residual value = Predicted value - Actual value
If the observed (actual) y value is 10, and the predicted value is 14. Then the residual value will be
Residual value = 14 - 10
Residual value = 4
The residual value will be 4. Then the correct option is D.
The complete question was attached below.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1

Please see screenshot.

Answers
Answer:
See below
Step-by-step explanation:

Am I correct because I’m confused

Answers
Answer:
you could be correct but I think it's B
Cold Beans wants to make a blend of their two best coffees, Guatemalan and Jamaican coffee. The pound of Guatemalan Coffee costs $11/lb and the other one costs $5/lb. If they want the cost of a 6 pound bag of blend to be $8/lb, how much Guatemalan coffee should they use per pound of the blend?
Answers
For each pound of the blend, Cold Beans should use 3 pounds of Guatemalan coffee.
This means that in a 6-pound bag of the blend, they would use \(3 \times 6 = 18\)pounds of Guatemalan coffee.
Let's assume that x pounds of Guatemalan coffee are used per pound of the blend.
Given information:
Cost of Guatemalan coffee = $11/lb
Cost of the other coffee = $5/lb
Desired cost of the blend = $8/lb
Total weight of the blend = 6 pounds
To find the ratio of Guatemalan coffee to the total blend, we can set up the equation:
\((x \times 11 + (6 - x) \times 5) / 6 = 8\)
In this equation, \((x \times 11)\) represents the cost of the Guatemalan coffee in the blend, and\(((6 - x) \times 5)\) represents the cost of the other coffee in the blend.
The numerator is the total cost of the blend, and we divide it by 6 (the total weight of the blend) to find the cost per pound.
Now, let's solve the equation for x:
(11x + 30 - 5x) / 6 = 8
6x + 30 = 48
6x = 48 - 30
6x = 18
x = 18/6
x = 3
Therefore, for each pound of the blend, Cold Beans should use 3 pounds of Guatemalan coffee.
This means that in a 6-pound bag of the blend, they would use \(3 \times 6 = 18\)pounds of Guatemalan coffee.
To summarize, to achieve a cost of $8 per pound for a 6-pound bag of blend, Cold Beans should use 3 pounds of Guatemalan coffee per pound of the blend.
For similar question on cost.
https://brainly.com/question/2292799
#SPJ8
a bit of help please?

Answers
The value of x for the chord is:
x = 12
How to find the value of x for the chord of the circle?A chord of a circle is a straight line segment whose endpoints both lie on a circular arc.
Recall that: If two chords intersect inside the circle, then they cut each other in such a way that the product of the lengths of the parts is the same for the two chords.
Using the above principle, we can say:
3 * x = 4 * 9
3x = 36
x = 36/3
x = 12
Thus, the value of x for the chord is 12.
Learn more about intersecting chords on:
https://brainly.com/question/13950364
#SPJ1
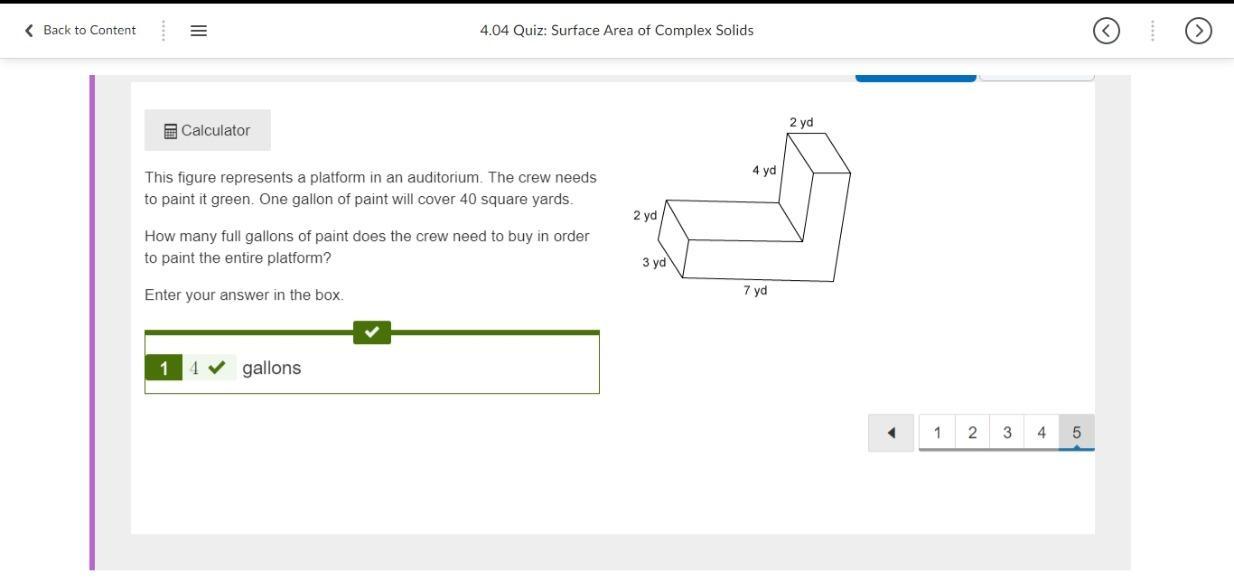
This figure represents a platform in an auditorium. The crew needs to paint it green. One gallon of paint will cover 40 square yards.
How many full gallons of paint does the crew need to buy in order to paint the entire platform?
Enter your answer in the box.

Answers
Answer:
4 i took the k12 quiz
Step-by-step explanation:

Answer: i swear people were saying it was 14 and 3 glad i got the right answer
Step-by-step explanation:
The Ozzie Chocolate Company is preparing to offer a new product in its candy offerings, the Minty Dark Chocolate Bite bar. Material costs per new candy bar are
$0.25 for chocolate, $0.02 for sugar, and $0.03 for mint flavoring. Labor costs of the new product are approximately $0.15 per bar. Adding a production line devoted to the new candy will cost $250,000 per year.
(a) If the sales price is $1.40 per candy bar, how many must the company make per year in order to break even? Assume that each bar made is sold at full price.
(b) What is the company's profit or loss if they make and sell 270,000 candy bars at the $1.40 price in the first year?
(c) About 20% of the food consumed in the U.S. is imported. Production in many industries has been offshored. What ethical issues do companies face when presented with the decision to move operations?
Answers
Answer:
a) 263,158
b) $164,500
c) Ethical issues companies face when deciding to move operations: job loss for employees, poor working conditions and exploitation of workers, negative environmental impact,...
Step-by-step explanation:
a)
Total cost = (0.25 + 0.02 + 0.03 + 0.15) x + 250,000
Total revenue = 1.40x
Setting the two equations equal to each other and solving for x, we get:
(0.45)x + 250,000 = 1.40x
0.95x = 250,000
x ≈ 263,158
b)
If the company sells 270,000 candy bars at $1.40 each, the total revenue generated is:
270,000 * $1.40 = $378,000
The total cost of producing 270,000 candy bars is:
(0.25 + 0.02 + 0.03 + 0.15) * 270,000 + $250,000 = $213,500
Therefore, the company's profit is:
$378,000 - $213,500 = $164,500
c)
Ethical issues companies face when presented with the decision to move operations: job loss for employees, poor working conditions and exploitation of workers, negative environmental impact,...
34. A motorist started a journey at 10.25a.m. and ended at 6.15 p.m. Calculate the time
used for the journey.
Answers
Write the times for each hour from start time:
10:25 am
11:25 am
12:25 pm
1:25 pm
2:25 pm
3:25 pm
4:25 pm
5:25 pm
6:25 pm
There are 8 hours between 10:25 am and 6:25 pm.
they finished at 6:15 which is 10 minutes before 6:25 ( 25-15 = 10)
10 minutes less than a full hour is 50 minutes ( 60 - 10 = 50)
8 hours - 1 hour = 7 hours
7 hours + 50 minutes = 7 hours 50 minutes total time.
Answer:
seven hours and 50 minutes
Step-by-step explanation:
For my friend I’ll mark you and thanks you

Answers
What is the range of the function f(x) = |x + 4| + 2?R: {f(x) ∈ ℝ | f(x) ≤ 2}R: {f(x) ∈ ℝ | f(x) ≥ 2}R: {f(x) ∈ ℝ | f(x) > 6}qqR: {f(x) ∈ ℝ | f(x) < 6}
Answers
Given the Absolute Value Function:
\(f(x)=|x+4|+2\)You need to remember that the form of an Absolute Value Function is:
\(y=a|x-h|+k\)Where "h" is the x-coordinate of the vertex, and "k" is the y-coordinate of the vertex. If "a" is positive the function opens up, and if it is negative, the function opens down.
By definition:
- If "a" is positive, then the Range of the function is:
\(R:y\ge k\)- If "a" is negative, the Range of the function is:
\(R:y\leq k\)In this case, you can identify that:
\(\begin{gathered} a=1 \\ k=2 \end{gathered}\)Therefore, you can determine that its Range is:
\(R:\lbrace f(x)\in R|f(x)\ge2\rbrace\)Hence, the answer is: Second option.
You can buy 20 pens for $8 or 30 pens for $10. Which is the better deal?
Answers
Answer: It would be the first one (20 pens for 8$)
Step-by-step explanation: If you divide 20 by 8 then each pencil will be 2.50$. However if you divide 30 by 10 it will be 3 dollars for each pencil so the first deal will be better since you spend less money.
Using the table below, solve f(x)=-69.2. separate multiple solutions with commas if necessary.

Answers
Answer:
x = 2
Step-by-step explanation:
Using a table
We want to find the value of x when f(x) = -69.2
From the table we see that when f(x) = -69.2, x = 2